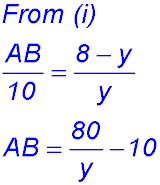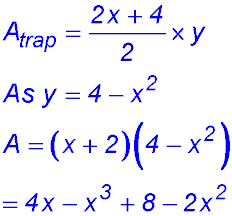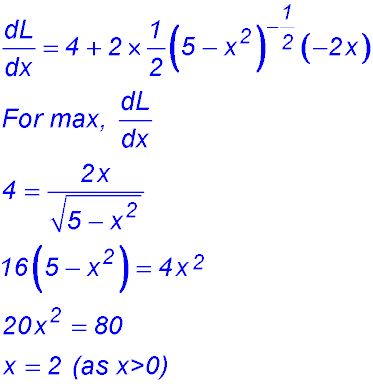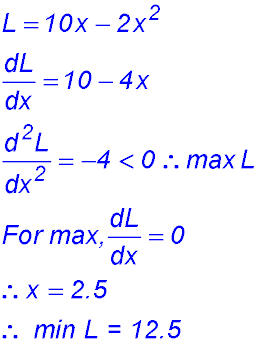Dr. J's Maths.com
Where the techniques of Maths
are explained in simple terms.

Calculus - Differentiation - Applied max/mim questions.
Type 2: 2D shapes - Test Yourself 2 - Solutions.


 

 
Creating two shapes. 1. (i)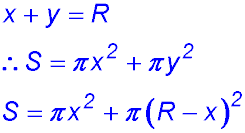

 

(iii)

(ii)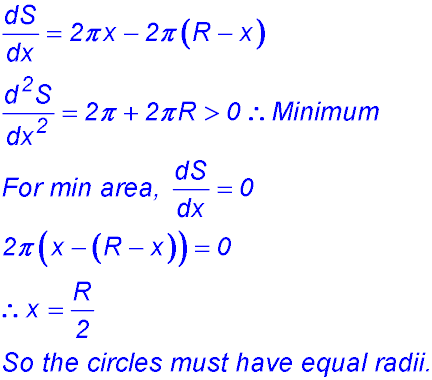
  2. (i)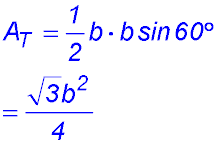

(ii)

(iii)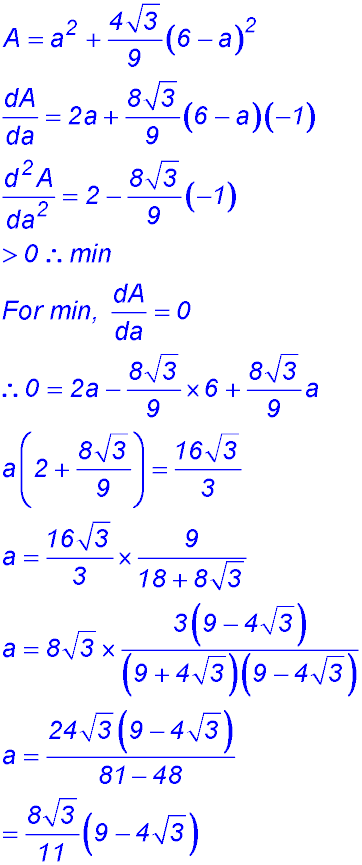
Paddocks and areas. 3. (i) PQ is simply the difference between the y values for the two curves
- i.e. the vertical distance.

So DPQ = (6x - x2) - (x2 - 4x) = 10x - 2x2.

 

(ii) Area = (10x - 2x2)× x =10x2 - 2x3.

 

 (iii)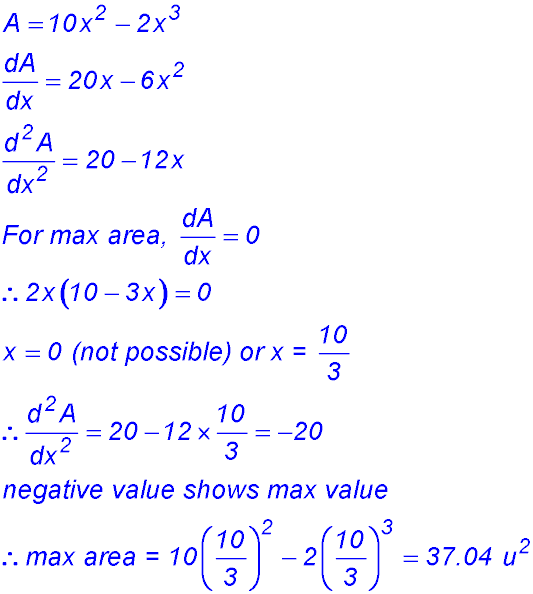
  4.

(i) Perimeter 376 = 2(x + a + y + b).

∴ a + b = 188 - x - y

(ii) Green Area = 6567 = xa + xb

6567 = x(a + b)

6567= x(188 - x - y)

188 - x - y = 6567x-1

∴ y = 188 - x - 6567x-1

 

 (iii) If the vertical height is a maximum:

  5.

 

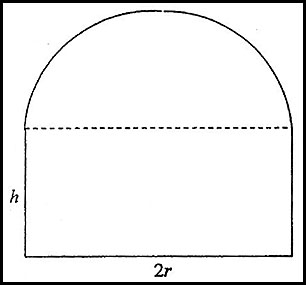
(i) The perimeter is P = 2h + 2r + circumference of the semicircle (of radius r).

 

 

 (ii)

(iii)
  6. (i) As the two areas are equal, the area of the big triangle ABC is twice the area of the smaller triangle AST.


(ii)

(iii)

 (iv) We need to find an expression for ST (= z) but the only expression we have has a cos A term. So we might have a hunch to try to eliminate the cos A and also use our result in (iii). So we could use the cosine rule again on the big triangle ABC:

  7.  
 

8. (i)

(ii)

(iii)

(iv)

β 2 √5 2.5
dA/dβ 0.74 0 -0.59

Change of gradient from +ve to -ve hence a maximum area of 6√5 at x = √5.
Geometric shapes. 9.

(i)

 

(ii) .

 (iii)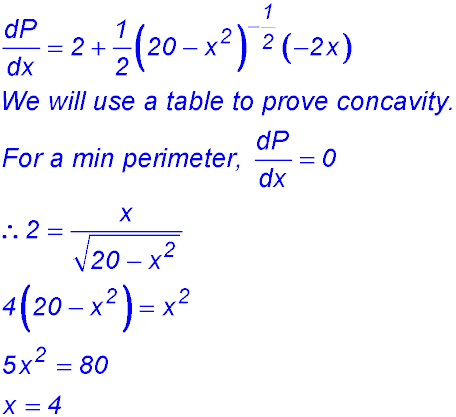
x 3 4 4.2
dP/dx 1.1 0 -0.73

∴ change of concavity from -ve to +ve - so minimum.

So the minimum perimeter is 14.47 m.

  10.

 

(ii)

(iii)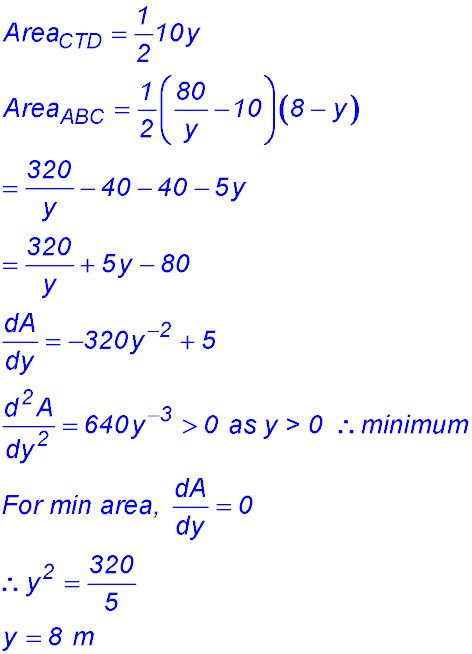
 

11. (i) R is (-2, 0) and S is (2, 0).

(ii) RS = 4 and QP = 2x

 

 (iii)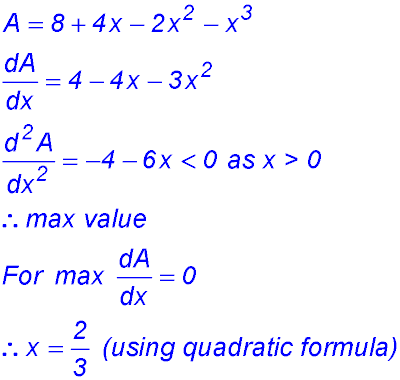
  12. (i)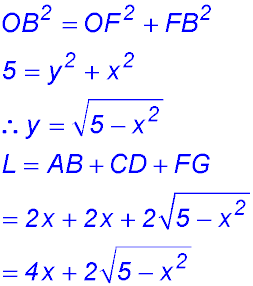

(ii)

x 1 2 2.1
dL/dx 3 0 -1.5

Change of gradient from +ve to -ve - so maximum length when x = 2.
  13. Draw verticals from C and D to AB. Join OC.

AE = FB = x - so EF = DC = 2R - 2x.

OC = R.

 
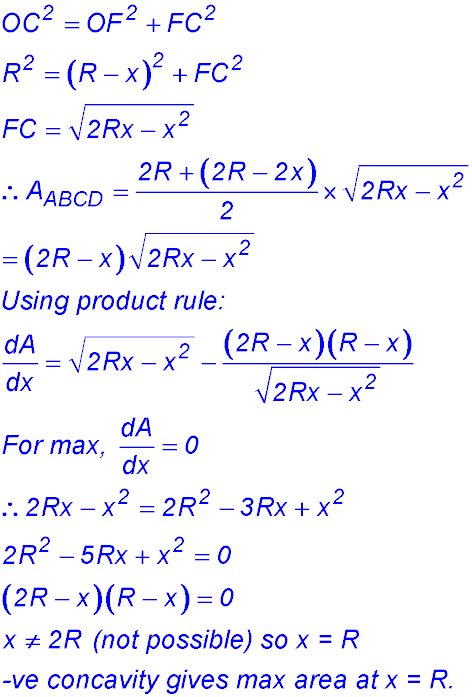Distance between 2 curves. 14. (i)
 

 

 
(ii) PQ = L = x(6 - x) - x(x - 4)

=6x - x2 - x2 + 4x

= 10x - 2x2

 

(iii)
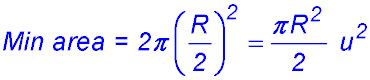
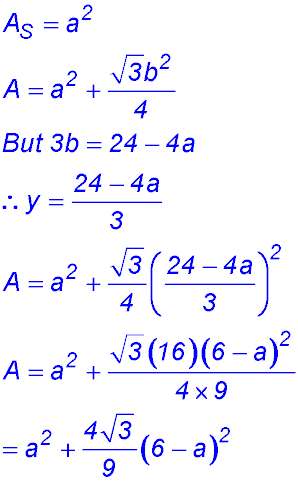
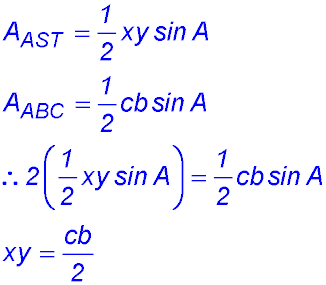
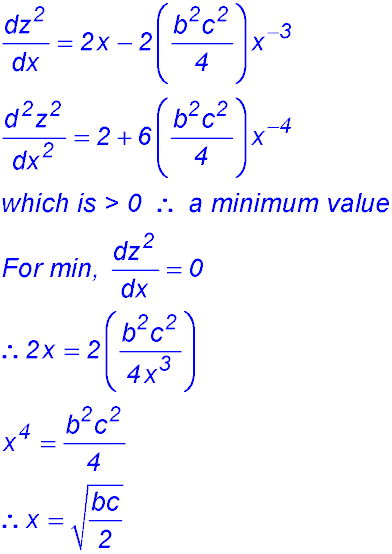
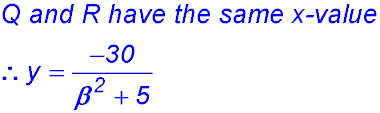
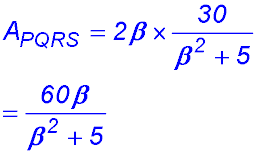
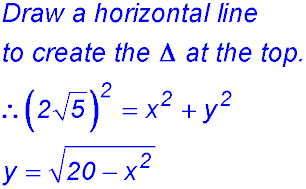
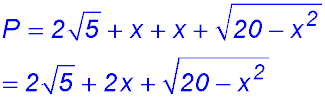